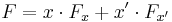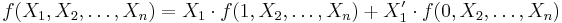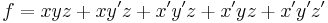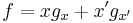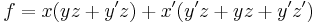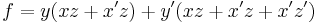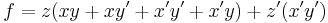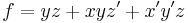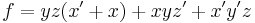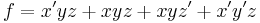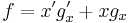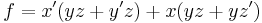Shannon's expansion
In mathematics, Shannon's expansion or the Shannon decomposition is a method by which a Boolean function can be represented by the sum of two sub-functions of the original. Although it is often credited to Claude Shannon, Boole proved this much earlier. Shannon is credited with many other important aspects of Boolean algebra.
Contents |
Expansion
The Shannon expansion develops the idea that Boolean functions can be reduced by means of the identity:
where  is any function and
is any function and 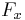 and
and 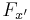 are positive and negative Shannon cofactors of
are positive and negative Shannon cofactors of  , respectively. A positive Shannon cofactor of function
, respectively. A positive Shannon cofactor of function  with respect to variable
with respect to variable  is defined as that function with all instances of
is defined as that function with all instances of  replaced by
replaced by 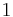 . A negative Shannon cofactor is the same, but replaces all instances of
. A negative Shannon cofactor is the same, but replaces all instances of  by
by 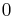 .
.
The Shannon expansion theorem is an important idea in Boolean algebra. It paved the way for binary decision diagrams, satisfiability solvers, and many other techniques relevant for computer engineering and formal verification of digital circuits.
Shannon's Jan.1948 paper, "The Synthesis of Two-Terminal Switching Circuits,"[1] simply stated the expansion of a function as:
followed by the expansion for two variables, and noted that expansion can be continued for any number of variables.
Example
Take this as our given function:
You can re-write the function in terms of any variable and its complement:
by simply applying the distributive property separately for the variable and for its complement, applying the associative and commutative properties as needed to factor out the selected variable:
Thus, we have "expanded the function f about the variable x."
The expansions of f about y and z are:
x Variables
In Shannon's expansion the term x is very significant but problems can arise in simple equations. What if there were no x variable in one or more of the terms? Problems here can lead to confusion. Dealing with no x variable in one or more of the terms can be simple. The solution is not always intuitive.
In Boolean algebra, you can AND any literal or term with 1, and still achieve the same truth value. With that in mind, let's look at this function:
If we desire to expand around the variable x, we simply don't have enough information in the first term to accomplish this task. So, what do we do? Remember what was said above: AND the literal with 1, or, in this case 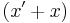 .
.
Expand:
This function contains the variable about which we want to expand the expression, so now we should have no problem performing the expansion:
The expansion is complete.
Of course, you can perform Shannon's Expansion about any variable you desire, so long as you can provide for that variable in the expression without changing the truth value of the expression. Also, you can perform multiple expansions of a single function (e.g. about x, then about y) or, you can even perform the expansion about many variables at once (e.g. about xy). The result is a functionally equivalent expression for the variables involved.
Expanding and minimizing
- You can expand a function
- You can minimize a function
Why make an expression larger? Is Boolean algebra all about minimizing functions?
Consider a logic device called a multiplexer. Multiplexers take n select inputs, and 2n data inputs, and give one output. Once you expand any boolean function about any number of variables, you can use the variables that the function was expanded about as the select inputs, and their respective composed functions as the corresponding data inputs.
See also
Notes
- ^ Shannon, Claude E.. "The Synthesis of Two-Terminal Switching Circuits". Bell System Technical Journal 28: 59–98.
External links
- Shannon’s Decomposition Example with multiplexers.
- Optimizing Sequential Cycles Through Shannon Decomposition and Retiming (PDF) Paper on application.